ResNet, apprentissage résiduel profond pour la reconnaissance d’images

Résumé

Les réseaux de neurones plus profonds sont plus difficiles à entraîner. Nous présentons un cadre d’apprentissage résiduel pour faciliter l’entraînement de réseaux nettement plus profonds qu’auparavant. Nous reformulons explicitement les couches comme l’apprentissage de fonctions résiduelles par rapport aux entrées, au lieu de fonctions non référencées.

Nous apportons des preuves empiriques montrant que ces réseaux résiduels sont plus faciles à optimiser et gagnent en précision avec une profondeur accrue. Sur ImageNet, nous évaluons des réseaux résiduels jusqu’à 152 couches, 8× plus profonds que VGG tout en restant moins complexes. Un ensemble de ces réseaux atteint 3,57 % d’erreur sur ImageNet. Ce résultat a remporté la 1ère place à l’ILSVRC 2015. Nous présentons aussi des analyses sur CIFAR-10 avec 100 et 1000 couches. La profondeur des représentations est centrale pour de nombreuses tâches de reconnaissance visuelle. Grâce à ces représentations très profondes, nous obtenons une amélioration relative de 28 % sur COCO. Les réseaux résiduels profonds sont à la base de nos soumissions ILSVRC & COCO 2015, où nous avons également remporté les 1ères places (détection ImageNet, localisation ImageNet, détection COCO, segmentation COCO).

• Article original : Deep Residual Learning for Image Recognition
• Dépôt GitHub : Deep Learning Classics: Read, Review, Recode

Contexte et problématique

L’idée dominante était : « plus le réseau est profond, mieux c’est ». Les réseaux de neurones ont pour avantage d’apprendre des représentations de bas, moyen et haut niveau. En théorie, la profondeur enrichit ces niveaux ; en pratique, la reconnaissance visuelle a beaucoup bénéficié des modèles très profonds.

Meme ResNet

« Apprendre de meilleurs réseaux, est-ce aussi simple qu’empiler plus de couches ? »

En bref : non. Les auteurs montrent empiriquement qu’en augmentant la profondeur, la précision se sature puis se dégrade : ajouter des couches à un modèle déjà assez profond augmente l’erreur d’entraînement et de test. C’est contre-intuitif : un modèle plus profond pourrait en théorie au moins égaler un plus shallow en copiant ses paramètres et en ajoutant des couches identité, mais en pratique ce n’est pas le cas.

Idée centrale : apprentissage résiduel

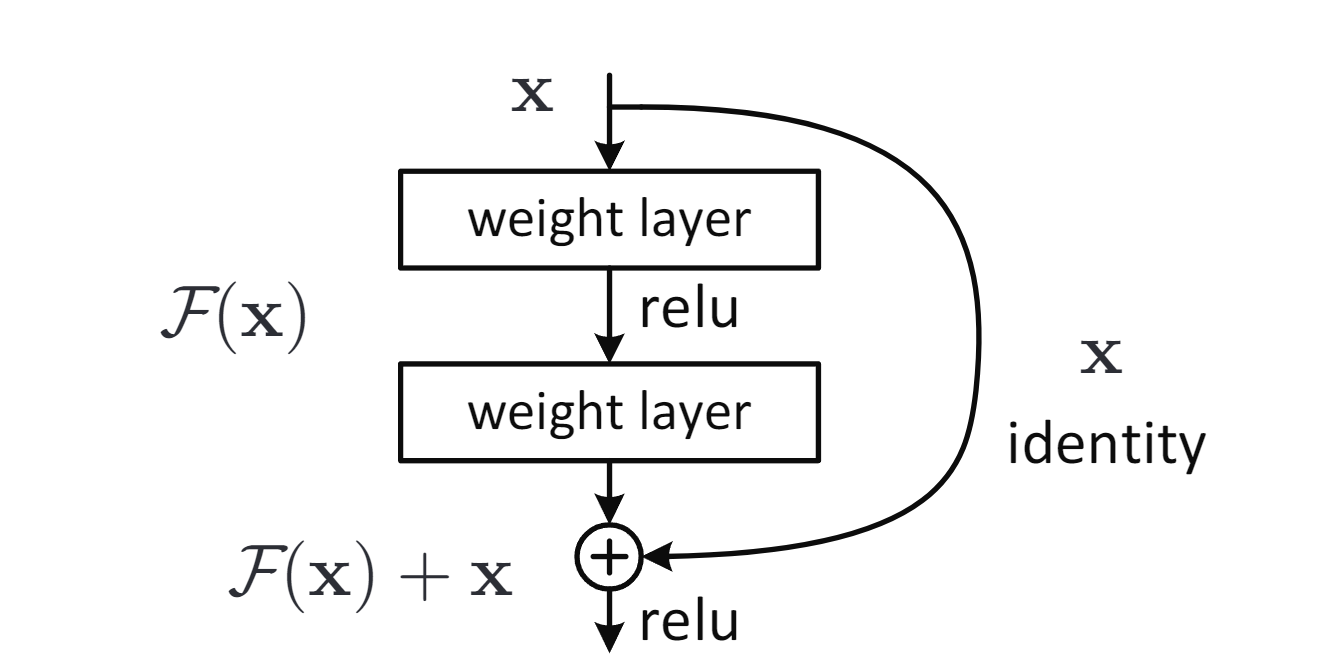
Le cadre d’apprentissage résiduel profond fait apprendre aux couches le résidu \(F(x) = H(x) - x\) au lieu de la fonction directe \(H(x)\), ce qui facilite l’optimisation ; la fonction d’origine est retrouvée comme \(F(x) + x\) via des connexions courtes identité, sans paramètre ni coût de calcul supplémentaires.

Apprentissage résiduel : un bloc de base.

Un bloc résiduel est défini par \(y = F(x, W_i) + x\), où $F$ est le résidu appris par quelques couches, et la connexion courte ajoute l’entrée $x$ à la sortie de $F$ par addition élément par élément ; aucun paramètre ni coût supplémentaire.

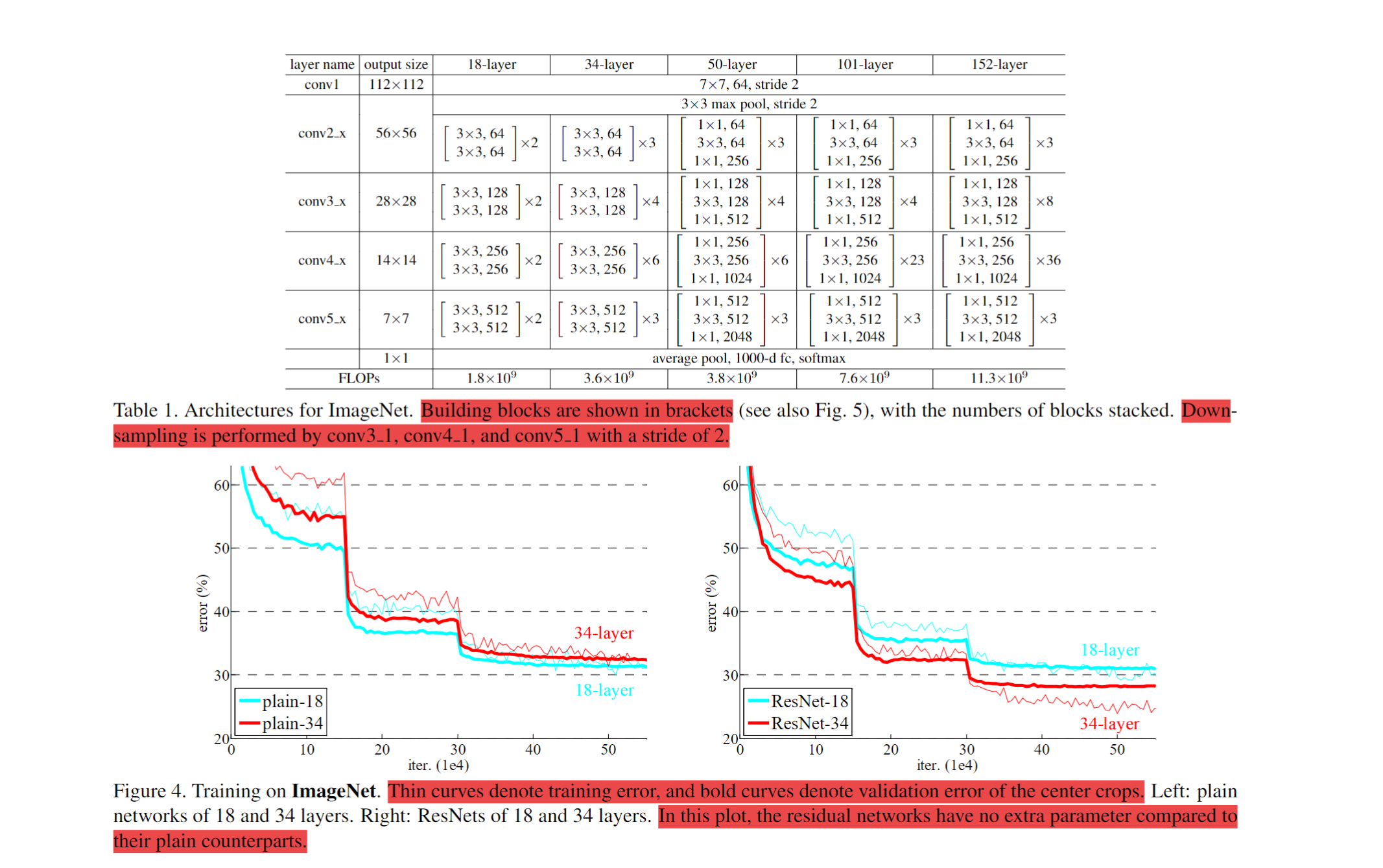
Les expériences sur ImageNet et CIFAR-10 montrent que : (1) les ResNets sont faciles à optimiser (convergence plus rapide), alors que les réseaux « plats » ont une erreur d’entraînement plus élevée quand la profondeur augmente ; (2) les ResNets profitent nettement de la profondeur et surpassent les réseaux précédents.

Points d’attention

Pour que les blocs résiduels soient cohérents, l’entrée $x$ et la sortie résiduelle $F(x)$ doivent avoir les mêmes dimensions ; sinon, une projection linéaire $W_s x$ est utilisée sur la connexion courte. Les mappings identité restent préférés pour leur simplicité et leur efficacité.

• Identité vs projection : trois stratégies ont été comparées (zero-padding, projection pour les dimensions croissantes, toutes les connexions en projection). Les projections n’apportent qu’un gain mineur par rapport à l’identité.
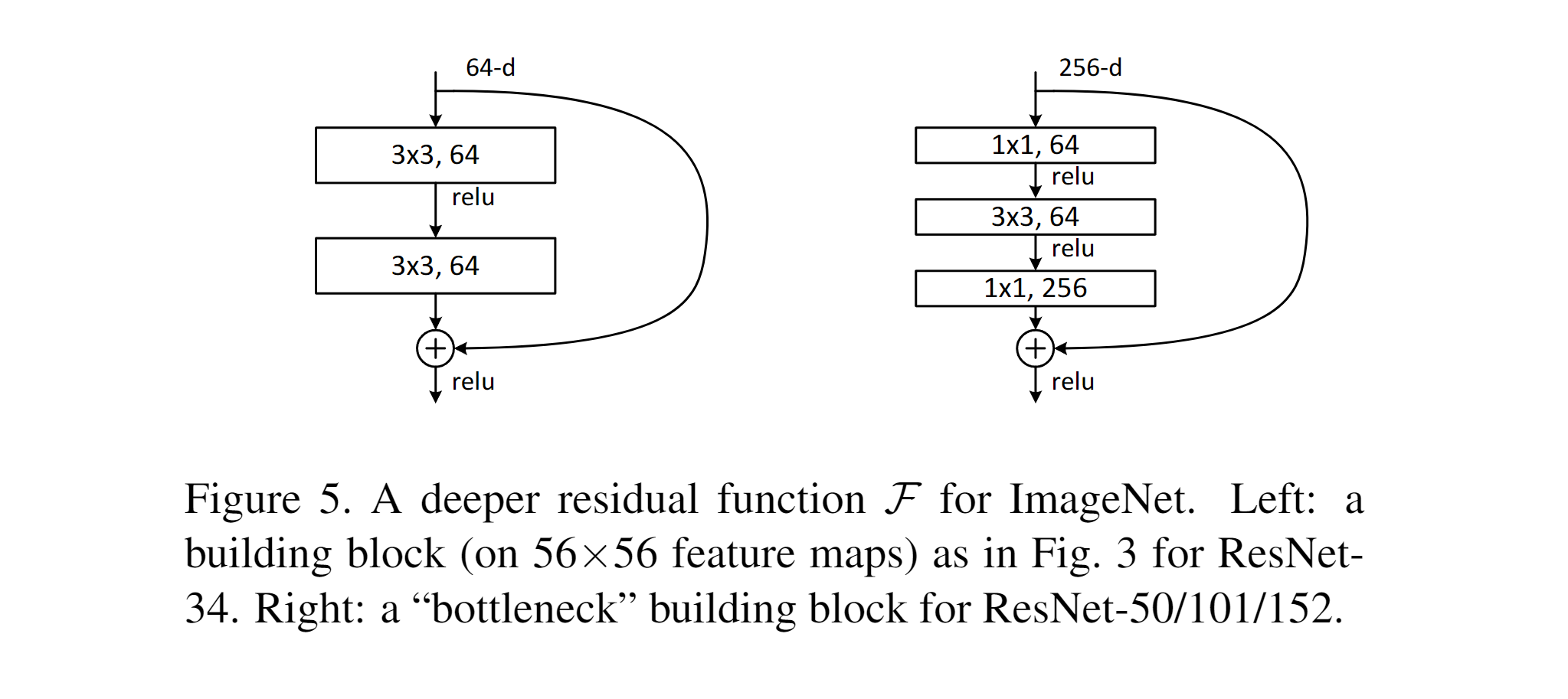
• Blocs bottleneck : pour accélérer l’entraînement sur ImageNet, un bloc bottleneck est introduit (1×1, 3×3, 1×1). Les connexions identité sont privilégiées pour l’efficacité.

Connexion résiduelle

Pourquoi ça marche ?

La dégradation suggère que les solveurs peinent à approximer des mappings identité par plusieurs couches non linéaires. Avec la formulation résiduelle, si l’identité est optimale, les solveurs peuvent simplement pousser les poids vers zéro. En pratique, l’identité n’est rarement optimale, mais la reformulation préconditionne le problème : si la fonction optimale est plus proche de l’identité que de zéro, il est plus facile d’apprendre les perturbations par rapport à l’identité.

Architectures et implémentation

Les réseaux résiduels sont construits en insérant des connexions courtes dans des réseaux plats. Connexions identité quand les dimensions entrée/sortie sont égales ; projection (1×1) ou zero-padding quand elles diffèrent. Les connexions qui traversent des cartes de tailles différentes utilisent un stride de 2.

Connexion résiduelle

Détails (ImageNet) : augmentation de données (côté court dans [256, 480], crop 224×224, flip), Batch Normalization après chaque conv, pas de Dropout, SGD momentum 0.9, batch 256, LR 0.1 divisé par 10 sur plateau, ~60k itérations, weight decay 0.0001.

Connexion résiduelle

Idées reçues

• La dégradation des réseaux profonds n’est pas due au surapprentissage.
• La Batch Normalization limite les gradients, donc ce n’est pas un problème de gradient.
• La difficulté d’entraînement vient plutôt d’une convergence lente que d’une dégradation du signal.

Ressources

• YouTube : Aladdin Persson, Professor Bryce, Maciej Balawejder, Yannic Kilcher, Priyam Mazumdar (implémentations et explications ResNet).
• À explorer : Batch Normalization (Ioffe & Szegedy, ICML 2015)